Crossing the Line - "When is the Right Time to Use Tied Notes vs. Whole Notes in Music?"

One of the most confusing things for the beginner musician to understand is the need for chopping up certain note values - such as a dotted crotchet - into smaller values - such as a crotchet and a quaver - and presenting them as tied notes.

This is because it seems that it can be very randomly allocated in the first instance. If I were to suggest to some pupils that they needed to notate a rhythm then strictly speaking they could do it correctly, but it would probably be wrong technically.

For example:

The above passage of music makes perfect sense - two dotted crotchets followed by a crotchet. If we break these down into quavers, it absolutely fits within the 4/4 time signature because a dotted crotchet = 3 quavers (remember a dot adds half a beat and, as we know, a crotchet is 2 quavers). So: 3 + 3 + 2 = 8! 8 quavers = 4 crotchets, so no issues there.

HOWEVER...it is wrongly notated...

The above passage - which is exactly the same rhythmically - is correct!

But why?

It's all to do with the idea of not 'crossing the line' and how we use tied notes to do this!

Let's investigate...

The Imaginary Middle Line in Music Notation

If we are in a time signature for which the top number is even - as many simple and compound time signatures are - 4/4, 2/4, 6/8, 12/8 - we can easily strike a line down the exact middle of the bar and keep it symmetrical. This is just simple mathematics - I need not even demonstrate with a bar of music yet to make the point!

4/4 - 1 - 2 (MIDDLE) 3 - 4

2/4 - 1 (MIDDLE) 2

6/8 - 1 - 2 - 3 (MIDDLE) 4 - 5 - 6

12/8 - 1 - 2 - 3 - 4 - 5 - 6 (MIDDLE) 7 - 8 - 9 - 10 - 11 - 12

You should be able to see the point - there are as many beats in the first half as in the second - perfect symmetry!

So now we just need to visualise the imaginary middle line on a piece of music:

On the above examples, we can clearly see a bar of each of the above time signatures divided up by its typical beats (the bottom notes of the time signatures - 4 = crotchet, 8 = quavers), as well as very clear indication of where the middle line is that splits them up!

So - to paraphrase the iconic rule from 'Ghostbusters' - we come to our first golden rule:

1. Don't Cross the Line!

Is this a hard and fast rule? Sadly not. Of course music has its little idiosyncrasies!

So how can we explain the rule so that its absolutely fail safe?

It all begins with our old friend symmetry once again!

Symmetry

If a note value crosses that line but splits in half so that it is the same on one side as the other - no need to split it up!

Why? I don't know...but this is standard.

However, if a note crosses the line but has a different value on each side of the line - now we need to split it!

To exemplify - some examples...

On the above example, we can see what can actually be interpreted as two correct forms of notation. Unlike the example below, it isn't actually a crime to tie two notes of equal value together - however, to be consistent with typical notation, the example above left with a rhythm of crotchet - minim - crotchet is accurate.

This is because - as the rhythmically identical bar following demonstrates - the minim is made up of two identical length of note (crotchets) on either side of the bar. Note how the 'imaginary middle line' splits that minim in half exactly. Therefore, no need for tieing our notes together.

The above example deals with a more syncopated rhythm - not dissimilar to the one at the very beginning of this post.

I have demonstrated the point clearly by marking out the 8 quaver beats in a bar below them to get us easily into the mindset of how long a dotted crotchet is (3 quaver beats).

As you can see from the example on the left, the second note - a dotted crotchet - crosses over beats 3, 4 and 5. Our imaginary line strikes the middle between beats 4 and 5, meaning that beats 3 and 4 of this note are on one side of the line and beat 5 on the other. The line has been crossed, and this is poor notation!

How do we solve this?

We break it up into two notes that won't cross the line and tie them together!

Beats 3 and 4 on one side are two beats - a crotchet, and beat 5 on the other is a quaver, so we notate them as two separate notes and tie them together!

Thus the rhythmically identical bar on the right is correct!

Further to the idea of symmetry within sections of the bar, don't forget that this also explains our use of whole bar notes / rests:

It would be unusual to see the above left notation of two minims tied together in 4/4. Because this is symmetrical, we can just substitute a whole bar note - in this case a semibreve.

Surely that's all we need to know to get this right?...

...sadly not!

Let's go further down this rabbit hole and discuss...

Tied Notes on Non-Syncopated Beats

For anybody who doesn't know about or of syncopation, that may fill you with dread.

However, its explanation is remarkably simple.

In a nutshell, syncopation refers to emphasising more strongly on the off beats (or playing between the beats - but for this example let's focus on emphasis). If we count 4/4, for example, as 1 - 2 - 3 - 4, then 1 and 3 are our on beats and 3 and 4 are our off beats.

So first beats are non-syncopated!

So why am I going on about it?

Because I want you to recognise where the non-syncopated beats are in the time signatures we have explored:

4/4 - 1 2 3 4

2/4 - 1 2

6/8 - 1 2 3 4 5 6

12/8 - 1 2 3 4 5 6 7 8 9 10 11 12

and consider these slightly more convoluted rules:

2. For /4 time signatures: Joining the Complete First Half of the Bar to the Second Half onto a Fully Recognised non Syncopated Beat = No Tied Notes Necessary!

3. For /8 time signatures: Joining the Complete First Half of the Bar to the Second Half onto any value in the second half (exception of the entirety!) = Tied Notes Necessary!

4. For /4 and /8 time signatures: We need to tie notes when joining a syncopated beat to a non syncopated one. We don't need to tie them when joining a syncopated to a syncopated or a non syncopated to a syncopated.

Don't panic - even my brain hurt as I tried to write those!

So let's break it down:

The complete first half of the bar means a note value that takes up the complete length of that bar.

In 4/4, for example, this would be a minim.

In 2/4, a crotchet.

In 6/8, a dotted crotchet.

In 12/8, a dotted minim.

A 'fully recognised non syncopated beat' in the second half means a note of the exact value of the lower numbers of the time signature (for example, in 4/4 - the lower number - 4 = crotchet) that falls on a beat we have identified as non syncopated in the second half of the bar (for example, beat 3 in 4/4).

Let's explore some examples:

The complete first half of the 4/4 bar above is correctly identified as a minim on the left, but then because beat 3 is fully recognised as the note value of a crotchet (the bottom 4 in 4/4), it actually means we don't need to tie - even though it crosses the middle line!

In this instance, we can use a dotted minim - therefore, the bar on the right - which is rhythmically identical - is better notation.

If we in any way disrupt the length of the first half of the bar, then we will of course have to resort back to tied notes:

In the case of 2/4, tying a crotchet (the entire first half of the beat) to beat 2 - regardless of its syncopation - gives us a whole bar's worth if this note is also a crotchet anyway:

However, with great ruling comes great controversy!

On the bars below, rule 4 actually takes over and dominates our understanding of symmetry. Symmetry would dictate that the bar on the left (below) was correct.

However, because beat 2 is considered the syncopated beat in 2/4, and our non syncopated first note on beat 1 ties to it, we don't need the tie! Therefore, the bar on the right is correct.

Let's see how this comes into play with 12/8:

In the above example, we can actually exemplify both rules 3 and 4:

• The first note in the bar on the left is 8 quaver beats (a semibreve) however, we now know that in 12/8 our middle line goes between beats 6 and 7 (as can be seen above with the line). So 8 beats starting at the beginning divides itself up by our first 6 beats and then another 2 - therefore a dotted minim and a crotchet. Notating it as these two notes tied together exemplifies both points 1 and 3.

• Point 4 deals with joining 2 or more consecutive beats together. After our first 8 beats, we can see on the left that we have a crotchet followed by two quavers to give us our final four beats. However, we know that beat 10 is a non syncopated beat, therefore needs marking as such in the music (on the example on the left, it is being swallowed up by the crotchet on beat 9). So that just needs splitting up into two notes that allow for beat 10 to shine. As it happens, in this example it is as simple as splitting this crotchet into two quavers.
  

Just to further exemplify the alternatives in rule 4, here is how a 12/8 bar should read divided into 'crotchets':

There is no fear of crossing the middle line here as the fourth note clearly begins on beat 7, however note that we have crotchets on beats 1 - 2, 5 - 6, 7 - 8 and 11 - 12.

We don't need to tie notes when they cross from a non syncopated to a syncopated beat (such as beats 1 - 2 and 7 - 8) or from a syncopated to a syncopated (such as 5 - 6 or 11 - 12).

However, we do need to tie them when connecting a syncopated beat to a non syncopated one - such as 3 - 4 and 9 - 10.

The 3/4 Waltz

You may have been wondering up to now - but what of the 3/4 time signature?

3/4 is divided very clearly into 3 crotchet beats, therefore its inclusion of an imaginary middle line is rather tricky.

Perhaps because of this, the ruling of the waltz / 3/4 time is much more relaxed, with the following examples being perfectly acceptable notation:

However, once you familiarise yourself with the above rules regarding other simple and compound time signatures, you will be able to recognise the similarities between 3/4 and 6/8 as printed music should you ever need to subdivide your 3/4 piece in quavers that cross certain lines at any time - and apply the rules accordingly:

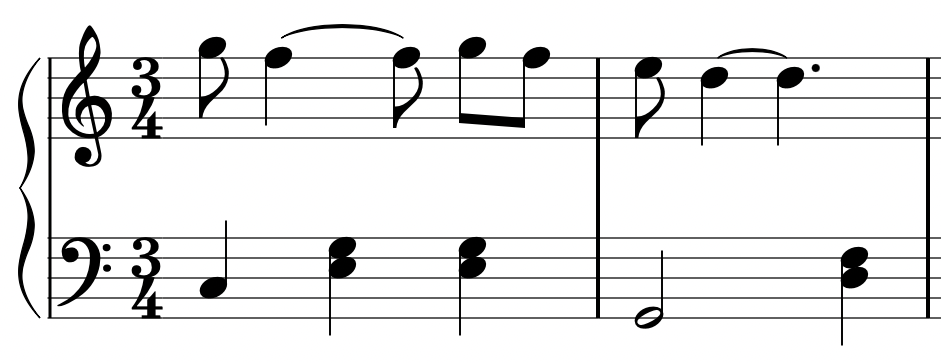
No doubt you can see above that - whilst we do want this to be in 3/4 time as opposed to 6/8 because of its very clear 3 beats in the left hand - we have incorporated a couple of tricks learned earlier into the right hand part:

Because this is subdivided into 6 quavers, the middle line is not crossed!

Irregular Time Signatures

I suppose all that's left now to explore is the irregular time signature. This is a complex one - aside from it being unusual to count anyway - as it can be differently interpreted by the composer / arranger.

An irregular time signature refers to an undividable number of beats - think prime numbers! The most common, therefore, are 5 and 7, and we often see 5/4, 5/8, 7/4 and 7/8.

However, we need to establish where the accents are in order to determine whether we will use tied notes and - if so - where.

For example, 7/8 can be counted 1 - 2 - 3 - 4 - 5 - 6 - 7 - 1 - 2 etc.,

But - being irregular - there is no clear definition of which beats are supposed to be emphasised and not. That is where we come in in the role of listener, interpreter, arranger, composer, performer etc.

We could establish that the music we are notating should emphasise:

1 2 3 4 5 6 7

or

1 2 3 4 5 6 7

or

1 2 3 4 5 6 7

and depending on where we put these emphatic beats - which we shall refer to as our non syncopated beats - affects how we would tie our notes.

We don't need to worry about our imaginary lines for irregular time signatures - just how our distribution of emphatic / 'non syncopated' beats affect them!

Therefore, the three examples above have been notated (respectively) using a demonstration rhythm. Note how we tie / don't tie notes in different places depending on where we consider the beats to be:

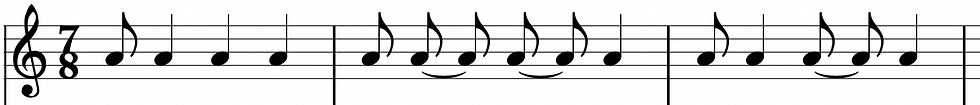
Conclusion - Tied Notes and Crossing the Line

If you aren't planning on notating music yourself any time soon, the above is all probably just academic as you can easily read two tied notes as easily as you can a whole one, wherever it lies in the bar. But it still pays to be aware of how it all works and how it all fits together - especially if you do decide to put pen to paper one day. I should point out, though, that - whilst these are the rules to follow - you can be forgiven for making simple errors of judgement and this will be entirely legible for the performing musician regardless. The more you familiarise yourself with it - through writing your own music and reading other transcriptions - the stronger your understanding of it will be!

As a further disclaimer, it should be observed that there is ongoing debate as to some of the lesson above. For example, many people would not cross a minim across beats 2 and 3 in a 4/4 bar and would still insist on its separation as 2 tied crotchets. This is fine, however I have personally come across more instances of the former over the years to have decided for myself that this is the rule I follow - so keep an open mind as you explore and investigate!

---

Jack Mitchell Smith is a piano teacher based in Macclesfield, Cheshire. Click here to find out more.

Weekly blogs are posted that may help you with your musical or piano journey. Click here to sign up to the mailing list so you never miss a post!

---

#pianolesson #musicnotation #sheetmusic #howtoreadmusic #musictheory #musiclesson #score #pianoscore

"The Ultimate Guide to Finding Chords on the Piano: Tips and Techniques"

When we begin our musical adventure, one of the great things we can start learning is chords. This is in no small part due to chords forming the backbone of much of the music we love - both contemporary and classical and all the bits in between!

When we start learning, we can make simple arrangements of our favourite songs using simplified versions of chords. By simplified, I refer to this because there are so many different types out there: sevenths, thirteenths, major sevenths, minor sevenths, sixths, suspended seconds and fourths, diminished and augmented (both of which can also be seventh), ninth, flat five - a lot! And when you consider that any note on the keyboard can be the root of a piano chord, it potentially seems a minefield of unlimited chordal possibilities.

However, most chords can be simplified to major or minor. We just need to know how to find them!

Let's explore exactly how we can do this...

Finding Major Piano Chords

It is highly unlikely that you don't know at least one major triad at this point. Usually, beginners will learn the C major triad to begin: C - E - G -but you may be so far into your learning that you've learn other such chords as F and G major as well.

Let's discuss how the chord is made up in one of two ways:

Intervals

Naturally, we will start our chord with the note of the chord we want to find.

So for C major, we need to find C. Because this is the note after which the chord is named, this is called the 'root note'.

Now let's think about the intervals between the notes from C to E and C to G so that we can find a rule that can be applied to other chords.

C to E is a third.

C to G is a fifth.

If you are counting in tones and semitones:

C to E is two tones.

C to G is three and a half tones.

If counting these in semitones;

two tones = four semitones

three and a half tones = seven semitones.

Remember:

• a semitone is the distance between a note and the note immediately right or left of it, whether that be a black or white note e.g. B - C / E - F / C - C#.

• a tone (or a whole tone) is two semitones, e.g. C - D / E - F#.

(Keeping the above structure as our reference, I want you to consider the importance of the third interval - the C to E - over the fifth interval as, as you will later discover, the fifth translates across both major and minor chords).

Scale

Another great way for finding chords is to remember - similarly to our interval numbering above - the numbers 1 - 3 - 5 and pick them directly out of the respective major scale.

The C major scale is:

C - 1

D - 2

E - 3

F - 4

G - 5

A - 6

B - 7

and as you can see, I've bolded the notes that are 1, 3 and 5: C - E - G.

Pro tip: if you use the scale such as the C major above and pick out chords from it using the same intervals (i.e. leaving one note between your three notes), you will pick out the chords based around each note respective to the very key signature that your scale is in. For example, if I use the C major scale above and start on D, then locate my next two notes using the same distance (leave a note between each) I get D - F - A. This is the D chord that fits into the key of C major. Remember that the scale repeats after 7, so if you run out of notes - just repeat!

Examples

Let's use the intervals method to find the chord of C# major.

Firstly, locate C#.

Then, we need to find the third and the fifth.

We've established that there are two tones / four semitones between C# and the third, so we need to count up four individual notes or two groups of two from this root note:

C#

D - 1

D# - 2

E - 3

F - 4

Now we can conclude that F is our third.

All we need to do now is find the fifth.

If you are good with intervals, you will already know what the fifth from C# is. However, if you need to count that's OK. But when you do, try and make a conscious effort to remember the intervals you are learning for quick reference in the future!

Let's count three and a half tones / seven semitones from C# to find the fifth:

C#

D - 1

D# - 2

E - 3

E# - 4

F# - 5

G - 6

G# - 7

And there it is! The triad of C# major is C# - E# - G#.

Now let's find the chord of E major using the scale of E major.

Our E major scale is made up - as is standard - of tone, tone, semitone, tone, tone, tone, tone, semitone (back into root / tonic).

Therefore:

E - 1

F# - 2

G# - 3

A - 4

B - 5

C# - 6

D# - 7

Our E major triad, therefore, is E - G# - B.

Finding Minor Piano Chords

We've now learnt how to identify any major triad on the piano.

Let's investigate minor chords the exact same way and see if we can spot any similarities!

Intervals

Due to it being the relative major of C, it isn't unlikely that you will learn A minor as your first minor chord. This is, therefore, the example that we are going to use.

Whilst working out our major chords, we already discussed the interval that is the fifth. The fifth is as true to a minor chord as it is to a major: remember how the interval of a fifth is called a perfect fifth as opposed to a major or a minor fifth, like most other intervals? This is because the distance on its own effectively creates an empty space that can be turned major or minor...

...and in the context of major and minor chords, it's the third that alters it:

The triad of A minor is A - C - E.

So let's explore the intervals.

A - E is a fifth, and this we can by now accept.

A - C is indeed a third, however

if we count this out using tones and semitones, you will find that you are counting one and a half tones / three semitones (as opposed to two tones / four semitones for a major chord).

This is because - although the interval is a third - it's now a minor third. The interval in C major of C - E is a major third!

So here comes a learning point for you:

• a major third is two tones / four semitones

• a minor third is one and a half tones / three semitones

So now we have established how many tones there are between the notes of a major and minor triad, it would be far more fitting at this stage for me to request you learn the intervals and then learn the simple rule:

Major Triad: Root - major third - fifth

Minor Triad: Root - minor third - fifth

If we decided to swap the majors and minors that we have learnt and apply our learning to find C minor and A major, those ahead of me will have already observed that there is a mere semitone between a major and a minor chord.

• To make a major chord minor, lower the third by a semitone.

• To make a minor chord major, raise the third by a semitone.

Therefore, C minor is C - E♭ - G

and A major is A - C# - E

Scale

Using A minor as our base again, let's just further exemplify how a scale can be used to pick out notes 1 - 3 - 5 of a standard chord.

If we wish to find an A minor chord, we need an A minor scale. If you have read my previous blog on the different types of minor scales, don't panic! You can use any of these as your basis, but I'm going to use the harmonic:

A - 1

B - 2

C - 3

D - 4

E - 5

F - 6

G# - 7

As you can see, 1 - 3 - 5 from the A minor scale means we can deduce that the A minor triad is A - C - E.

Examples

Let's use the intervals method to find F minor:

Finding the minor third from our root note - F - is as straightforward as counting up three semitones / one and a half tones:

F

G♭ - 1

G - 2

A♭ - 3

Now we have found F - A♭, we just need to find the fifth.

If we don't already know the interval, we can count three and a half tones / seven semitones to learn it!

F

G♭ - 1

G - 2

A♭ - 3

A - 4

B♭ - 5

B - 6

C - 7

And there we have it. F minor is F - A♭ - C.

Let's use the scale of A♭ minor to pick out 1 - 3 - 5 and find an A♭ minor chord:

A♭ - 1

B♭ - 2

C♭ - 3

D♭ - 4

E♭ - 5

F♭- 6

G - 7

So the triad of A♭ minor is A♭ - C♭ - E♭.

Creating a Fifth Piano Chord

Somebody asked me a few weeks ago is it were possible to have a chord of just two notes.

Answer: Kind of.

Strictly, this would be an interval. However, you can officially consider it a chord if at least one of those notes is played across two or more different pitches.

The most common example here is the fifth chord.

To create a fifth chord, all you need to do is remove the third and replace it with one of the existing notes you are playing at either a higher or lower pitch.

This would then be written using the root note followed by 5. For example, a C fifth chord would be written as C5.

Using C as an example, we will remove the third note (E or E♭, depending on whether you are thinking C major or C minor) and now you are left with the interval - a perfect fifth: C - G.

Now add another C either at the top, or a G at the bottom (or both - you can use both hands) and you have created a C5 chord!

C5 - example one

C5 - example two

Sometimes block major or minor triads can sound a little heavy, so a fifth chord is a great way to give your music breathing space. It is also a great alternative for performing instead of a chord you aren't familiar with.

For example, an F7sus4 requires one additional and one substituted note from your typical F chord. You may not know that yet, however, so until you do - an F5 will sound OK in its place because it removes the third, which is the note that is being substituted in the more complex chord above.

Inversions and Bass Notes

Now you have discovered the triads, play around with inversions.

An inversion is simply where you reorganise the same notes i.e. putting a different note in the bass.

For example, C - E - G is known as C major root position. Reorganising that to E - G - C is now C major first inversion, and reorganising again to G - C - E becomes C major second inversion.

When a chord is written as an inversion, it is done so by the simple use of a forward slash followed by the note name that is in the bass. For example, a C major second inversion would be written as "C / G" (remember we only specify tone when it is minor, and this would be done so using the letter 'm'. For example. C minor would be written as 'Cm'. If this isn't written, we can assume major).

Additional Bass Notes

The same pupil who asked me about two notes being a chord also asked me if a chord can be more than three notes.

They certainly can!

One simple way that we can explore these is to add a different note into the bass each time. You can use two hands for this exercise as it's more a familiarising and listening one, but try playing the following melancholic chord structure:

Am

Am / G

Am / F

Am / E

or a slightly more upbeat one:

C

C / Bb

F / A

Fm / A♭

G

Note how the bass note doesn't have to be part of the triad we have learnt. We're adding an extra note!

And whilst it's true to say that you are creating chords that might have more technical names than I've given above, this is an exciting way of hearing how different notes can create different effects on the simple triads you already have.

Keep your eyes open for more blog posts where I explore more complex types of chord and how they can help develop your music. Meanwhile, however, enjoy playing around with these basic triads and explore how different chords sound when put together.

---

Jack Mitchell Smith is a piano teacher based in Macclesfield, Cheshire. Click here to find out more.

Weekly blogs are posted that may help you with your musical or piano journey. Click here to sign up to the mailing list so you never miss a post!

---

#musictheory#piano #pianist #pianoteacher #pianochords #pianolesson #learnpiano #beginnerpiano #playpiano #pianopupil

Unfolding the Intrigue: The Extraordinary Tale of a Folding Piano

I've never been one of those piano purist teachers. Never...

Electric pianos and keyboards receive an awful lot of bad press for being too unlike the real thing, and whilst I agree that they certainly are unlike the real thing - and do in fact stand by my mantra that the closer your instrument to the real thing, the better - I am also very aware of the problems that they carry and create;

• Pianos are expensive

• Pianos are loud

• Pianos take up lots of space

• Pianos require maintenance

Probably the four main ones, listed above.

So in this day and age, I do stand by the following beliefs:

• Buying an electric piano or even a 61 key keyboard is OK if you are testing the waters. Until you're absolutely convinced, a piano - and even an electric piano, for many people - is too much of a gamble to take as a beginner.

• Buying a keyboard is sometimes the only way to go. Many modern houses - and apartments in particular - aren't designed for something as bulky and as loud as a piano.

• It is far better to sacrifice things such as number of keys, weight of keys etc. in the first instance than repressing your desire to learn the instrument. I myself learnt on a Yamaha PSR 290 up until Grade 5, by which time I was finally taken seriously enough to be bought an electric (a Casio Priya PX 700).

Note: I did do a blog here about the differences between acoustic and electric pianos, and if you are looking at which to invest in, give it a read as it will give you a good checklist as to what to look for for the best results.

Yet time and time again I am finding myself hearing the contrary from other piano teachers, pupils, reading other blogs and articles etc., which make me doubt myself. They say it is absolutely essential to learn on a piano from the start.

So it fills me with joy whenever I have success stories to share. And last week I was presented with one such story:

One of my pupils came to me to learn piano casually having received a digital keyboard for Christmas. She has been making good progress, but quite understandably the difference between the keys on a keyboard and on a piano do rear their head and make themselves known when she plays on my piano. At first it was rather timid in sound, because the keys on a keyboard are by nature more forgiving (they are programmed to always give a nice clean sound, whereas the hammer action on a piano responds much less predictably if you don't give a satisfactory velocity on the key).

This particular pupil has family overseas. Far overseas. And thus it is logical that she does need to go over for fairly extended periods of time (4-5 weeks, give or take) a couple of times a year. The first time this happened during her session of lessons wasn't too detrimental to her learning anyway. However, the time that she has just visited, she prepared herself.

A few weeks prior, she informed me that she had purchased a folding piano. Of course, I've seen these online but have never actually tried one. Naturally, she was already aware that it was no substitute for piano - or even her existing keyboard - because, as she said, the keys are squatter and overall smaller, naturally, but as we agreed (and - in similar vain to my points above) - if you need to practice, it is better to practice on something than nothing.

I was delighted to see this pupil again last week after 5 weeks, and all the more so when she told me that - thanks to this piano - she had been able to practice some exercises and pieces from her workbook and keep refreshing her memory of the pieces she is learning ('Für Elise' and 'Canon in D').

So she turned to the first piece in her book that she had been looking at and played it. And what an improvement from any of her performances of that piece in the past! -

• more confident dynamic

• more evenness across the fingers in playing chords (notes all played at the same time and all the same volume)

• a more upbeat tempo

The whole thing was a remarkable improvement, and as she observed;

'Perhaps it was the need to hit the keys harder to get a result from the folding piano that improved the technique enough to translate to a real piano'.

(paraphrased - I'm not in the habit of recording my pupils!)

And on that note, she left me said keyboard to try for myself. As you can see, the picture above of me - mid-move and in casual attire to show for it - could not resist the urge to try this.

So I did...

And I have to say, I agree.

Is it a great sound?

No.

Are the keys uncomfortably small?

Yes.

Is it an ideal practice piano?

Not even that!

But regardless, it did something for my pupil that improved her confidence playing on my piano (a real piano).

And so, for as much as people may worry over an electric piano that is literally recognised as the closest-to-the-real-thing-as-you-can-get being 'not good enough to learn properly on', I think this story highlights the unsung benefits of using what resources we can get rather than just saying 'no' outright.

(If I'd have said no on this principle, I'd never have played piano because our house just wouldn't have fit an acoustic one in!)

---

Jack Mitchell Smith is a piano teacher based in Macclesfield, Cheshire. Click here to find out more.

Weekly blogs are posted that may help you with your musical or piano journey. Click here to sign up to the mailing list so you never miss a post!

---

#piano #keyboard #pianolesson #pianist #pianoplayer #pianopupil #learnpiano #pianoteacher #macclesfield #congleton ..